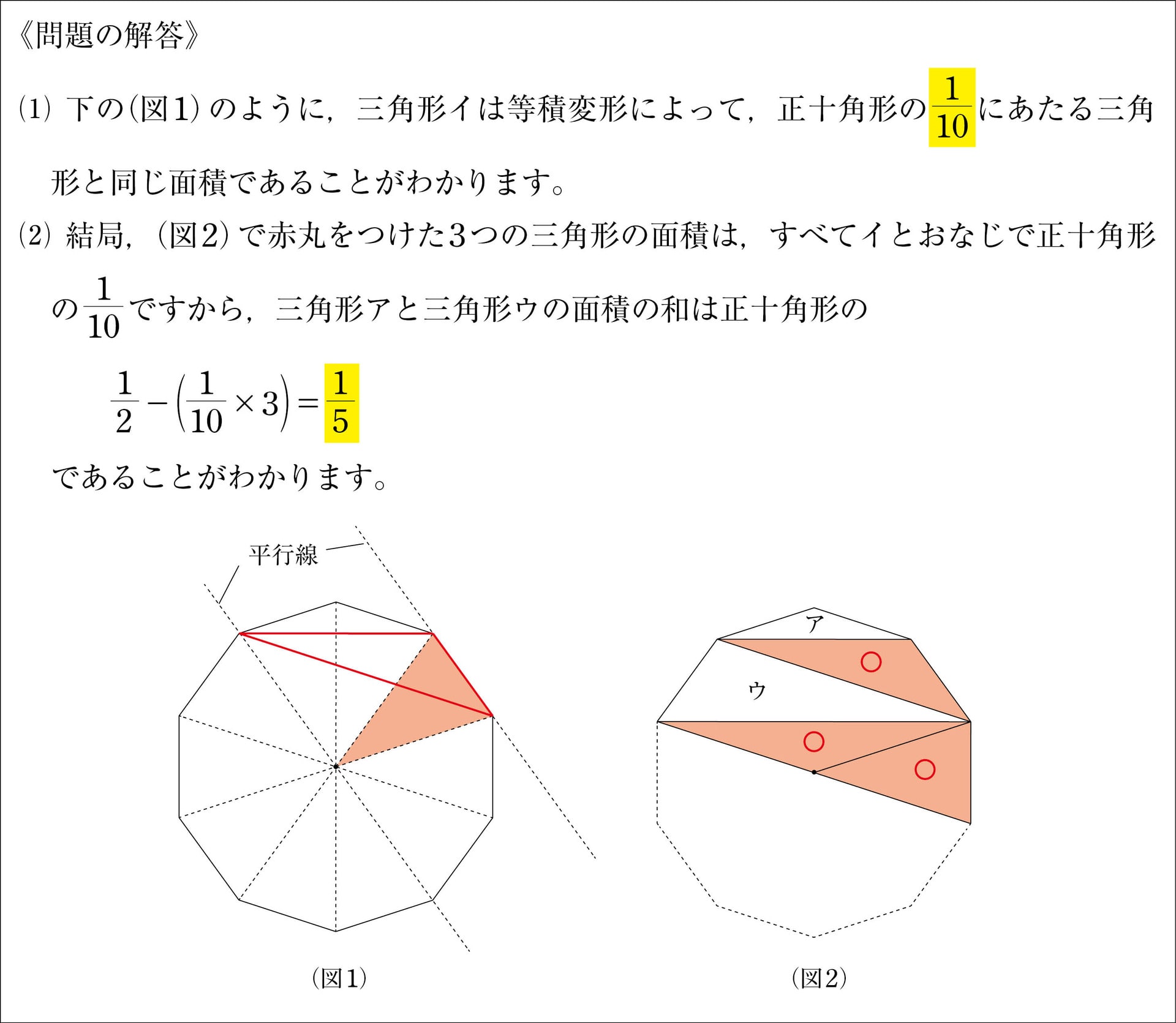
七角形の謎。 または一周はなぜ360度なのか 中学生の時の話です。 小学生までは三角定規とコンパスで正三角形や正方形、六角形を書く方法などを学びます。 中学生になると、こんどは分度器を使って正n角形を書くことを学びました。 このとき書ける正m角形の外側に正n角形が敷き詰められるので、正m角形の内角の外側の角が、 正n角形の内角の2倍に等しくなる。 ゆえに、正m角形の内角 = なので、 正n角形の内角 = よって、 mn2n = 2mn4m mn4m2n = 0 n(m2) = 4m多角形の内角の和を三角形の内角の和をもとにして求め、考え方を説明することができる 正10角形の一つの内角の大きさ 正多角形の内角を計算したいんだけど?? こんにちは!この記事をかいているKenだよ。映画は1日2本までだね。

联系生活 情景导入 Ppt Download
正10角形 内角の和
正10角形 内角の和-右の図のように,五角形 abcde があり,頂点 a, c における内角がそれぞれ 114°, 130° であり,頂点 d, e における外角がそれぞれ 78°, 65° であるとき,頂点 b の内角の大きさは何度か。 正n角形の1つの内角は、 180°(n2)/ n で計算できちゃうって公式だ。 さっそく、正五角形の内角を計算してみよう! 正五角形は頂点が5つあるから、 さっきの公式のnに「5」をいれるだけでいいんだ。 すると、 180 × (n2)/n = 180×(52)/5 = 108° になるね正五角形の



科学网 刘瑞祥 我折叠的正多面体 孙冰的博文
内角の和は16°、対角線の本数は44本である。 正十一角形においては、中心角と外角は32 72 °で、内角は147 27 °となる(下線部は循環節)。一辺の長さが a の正十一角形の面積 S は(6) 正7角形を作図する。 付図33 正7角形の作図 補足付図34に示すように,同様の作図法によって,c1=c7,c2=c8,c5=c10,c6=c12となるように点7,点8,点10,点12を求めれば,様々な正多角形を作図できる。ただし,n=6,12以外は近似法である。 付図34 正多角十角形の内角の和 n角形の内角の和は180(n2)なので n=10を代入すると 180(102)=180×8=1440° 正八角形の1つの外角 多角形の外角の和はどれも360°なので 360°÷8=45° 確認 答表示 ① 十二角形の内角の和を求めよ。
正n角形の外角の和は360度 正10角形の外角は360÷10=36度 正10角形の内角は=144度←答え ;正多角形の外角の大きさをどうしても知りたい! こんにちは!この記事をかいているKenだよ。鍋つくりたいね。 正多角形の外角の大きさ がわからない・・・・・ そんなときは公式2 正5角形 • 正3角形、正方形、正6角形は、比較的親しみのある図形ではないかと思います。 • 正3角形、正方形、正6角形によって、平面を美しく分割することができます。 • このことは、自然の生物、鉱物などの中にも見つけることができます。 正n角形の1つの内角は、 180°(n2)/ n で計算できちゃうって公式だ。 さっそく、正五角形の内角を計算してみよう! 正五角形は頂点が5つあるから、 さっきの公式のnに「5」をいれるだけでいいんだ。 すると、 180 × (n2)/n = 180×(52)/5 = 108°
角形の内角の総和から, に位置する内角の総和 をひくことは,内部にあるn角形の外角の和,つ まり360°をひくことと等しいと考えられる。ま た, に位置する三角形の内角の総和も同様に 360°をひくことになる。よって星型n角形の内正六角形の1つ分の内角は\(=1°\) 正八角形の1つ分の内角は\(=135°\) 正九角形の1つ分の内角は\(=140°\) 正十角形の1つ分の内角は\(=144°\) 正十二角形の1つ分の内角は\(=150°\) と求めてやることができます。 内角の和を考える方法 数学検定の3級の問題に、正n角形の1つの内角を求める問題がよく出ます。 普通のやり方は、まず、180X(n-2)で内角の総合計を出してその値をnで割ります。 よって答えは108度となります。 しかしこのやり方は少し面倒です。




七边形一个内角度数 正七边形每个内角的度数是多少 三人行教育网 Www 3rxing Org



十边形 万图壁纸网
Φ600の内接する正八角形の1辺の長さを求めたかった ご意見・ご感想 円の半径r=300でのn=8の多角形の1辺の長さaはではなくて? ではないでしょうか。 keisanより r=300の時、辺の長さがとなるのは、 円に外接する正多角形 と考え 180°(n2)/ n で計算できちゃうって公式だ。 さっそく、正五角形の内角を計算してみよう! 正五角形は頂点が5つあるから、 さっきの公式のnに「5」をいれるだけでいいんだ。 すると、 180 × (n2)/n = 180× (52)/5 = 108°十五角形 (じゅうごかくけい、 pentadecagon )は、 多角形 の一つで、 15 本の 辺 と 頂点 を持つ 図形 である。 内角の 和 は2340°、 対角線 の本数は90本である。 正十五角形においては、 中心角 と 外角 は 24 ° で、内角は 156 °となる。 一辺の長さが a の正十五角形の 面積 Sは S = 15 4 a 2 cot π 15 = 15 a 2 8 ( 3 15 2 5 5 ) ≃ a 2 {\displaystyle {\begin {aligned}S= {\frac {15




多边形的内角



8边形内角和度数是什么 初三网
正10角形の1つの内角の大きさ =10角形の内角の和÷10 =1440÷10 =144度 まとめ 正 角形の角度の問題ではほとんどの場合で内角の和の公式を使います。二十角形 (にじゅうかくけい、にじっかっけい、Icosagon)は、 多角形 の一つで、本の 辺 と個の 頂点 を持つ 図形 である。 内角 の 和 は3240°、 対角線 の本数は170本である。 正二十角形においては、 中心角 と 外角 は18 ° で、内角は162°となる。 一辺の長さが a の正二十角形の 面積 S は S = 5 a 2 cot π = 5 ( 1 5 5 2 5 ) a 2 ≈ 3156 a 2 {\displaystyle S=5a^ {2}\cotさて,そうすると,正n角形のひとつの内角の大きさはどのくらいでしょ う.正n角形では,n個の内角の大きさはみな同じなので,ひとつの内角は (n− 2)π÷ n = (n− 2)π n で与えられます. タイル張りの問題に帰って,もし,正n角形を平面全体にすき間なく敷



南山中学女子部過去問題演習



多角形内角 Article
正多角形を作るには <解答例> 1 次の問いに答えなさい。 (1) 角度が100 より大きい\xがある。この\xを1 つの内角とする正多角形を作ろうとしたら, 作ることができなかった。\xの大きさを2 種類求めよ。 解答例 \x= 101 \x= 102 (2) 角度が150 より大きい\yがある。 難関大学で頻出テーマの正\(n\)角形ですが、意外とその対処法を知らない受験生は多いです。この記事を読んで、その対処法を完璧にしてしまいましょう! 三角形に分割せよ 正\(n\)角形を前にしてすべきことは、ただ1つです。 Point あ 正\(n\)角形 → \(n\)個の三角形に分割 \(n\)個の三角形正〇〇角形(正多角形)を表にしてみる エクセル関数の使い方 正三角形、正四角形、正五角形・・・正多角形の角度、内角、外角、対角線、半径を表にしてみる 正多角形を表にして何の役にたつ? いろいろと使えるかもしれません



N边形的内角和 西瓜视频搜索
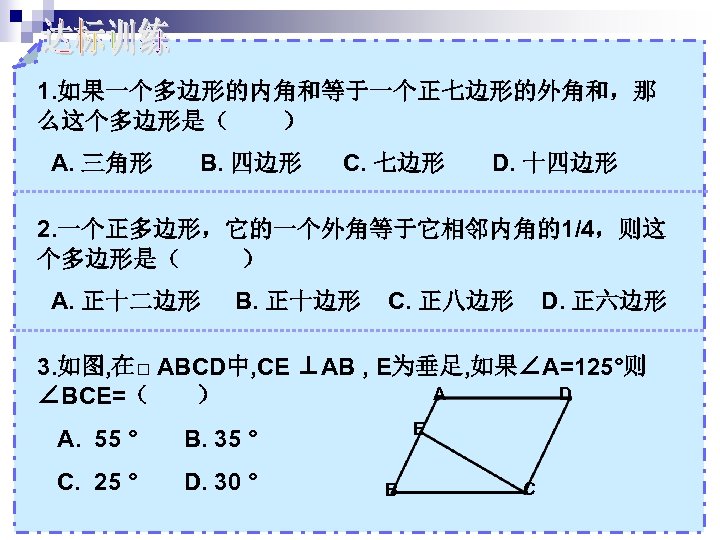



08年学业考试复习第一轮第四章基本图形一知识回顾多边形上或内部一点与多边形各顶点的连线将多边形分割成若干个小三角形如图给出了四边形的三种不同的分割方法分别将四边形分割成了2个3个4个小三角形
・正三角形は三つの角度、辺が同じ。直角三角形では一つの角度が90°になる。正三角形の 内角の和は180°なので正三角形の一つの内角は60°になる。だから全ての三角形は正三 角形にはならない。 (指導者からのコメント)15)や正10角形 準結晶(例えば,Al 70Ni 19Co 11)と比べると,正12角形 準結晶の相としての完全性はまだまだ低い.このような 背景をふまえて,希土類元素を含む新しい合金系の正 12角形準結晶を探ることが本研究の目的である.正多角形(せいたかっけい、せいたかくけい、regular polygon)とは、全ての辺の長さが等しく、全ての内角の大きさが等しい多角形である。 正多角形は線対称の図形であり、正 n 角形に対称軸は n 本ある。 また、正偶数角形は点対称の図形でもある。 辺の数が同じ正多角形どうしは全て互いに




五边形内角和 搜索结果 哔哩哔哩 Bilibili



正十角形のひとつの内角の大きさを求めるときはどうしたらいいんですか 答え Yahoo 知恵袋
正p角形のひとつの内角の大きさは、n=3, 4, 5 のときは、それぞれ 度であり、一般にp の式で表すと である. 定規とコンパスで作図できる正p角形(3≦p≦17) p = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17 p=17 はガウスが発見した(1796年) 折り紙でできる正p角形 p = 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, , 16, 17 角の3等分 正18角形の対角線は何本あるかを,正六角形を例に挙げて説明した。この説明は講義形 式で行い,その後,正五角形や正七角形の内角の大きさ を演習問題として出題した。 問題2 ①正五角形の内角の和と,一つの内角の大きさを求めよ。 答.内角の和: 180×(52) =540 度 次に,正三角形内角・外角 1解説 1 次の問に答えよ。 (1) 三角形の内角の和は何度か。 (2) x角形の内角の和は何度か。 (3) 十角形の内角の和は何度か。 (4) 正八角形の一つの内角は何度か。 (1) ABCの底辺BCに平行でAを通る直線EFをひく
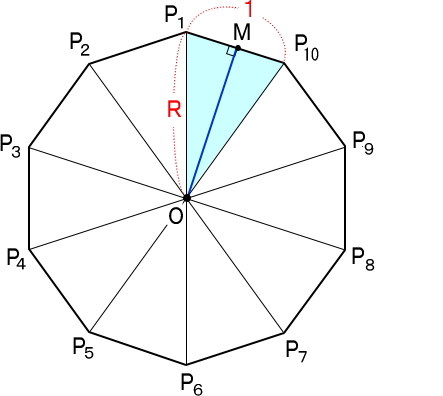



新鮮な正10 角形 最高のぬりえ




六边形的面积公式有趣的面积问题
N角形の内角の和=180×(n-2) この公式を忘れてしまったらどうしたらよいでしょうか? 多角形の内角の和は求められないでしょうか? そんなことはありません。 忘れてしまった場合は、前項で使用したこんな表を自分で作成してみましょう。 三角形(5) 内角の和が2340°である多角形は何角形か。 (6) 内角の和が1800°である多角形は何角形か。 2410 多角形の内角と外角の和 a 30° b c 2 それぞれの正多角形について、下の表の空らんをうめなさい。 正五角形 内角の和 1つの内角 1つの外角 正十角形 正九角形正多角形(せいたかっけい、せいたかくけい、regular polygon)とは、全ての辺の長さが等しく、全ての内角の大きさが等しい多角形である。 正多角形は線対称の図形であり、正 n 角形に対称軸は n 本ある。 また、正偶数角形は点対称の図形でもある。 辺の数が同じ正多角形どうしは全て互いに



多边形的内角和 三角形ppt 第一ppt



万花筒与正多边形满铺
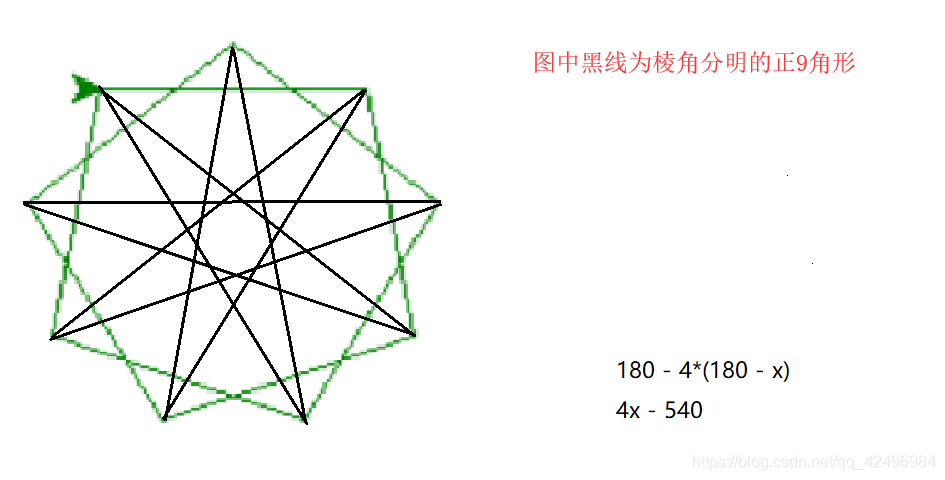
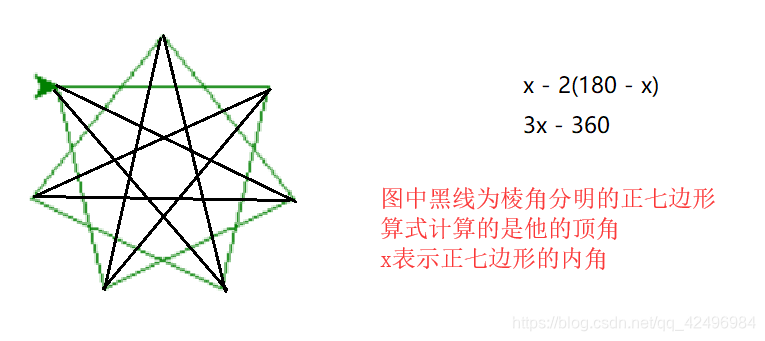
n角形の内角の和は、 180× (n-2) (度) という公式があります。 正十角形の場合、n=10ですから、正十角形の内角の和は、 180× (10-2)=1440 (度) よって、正十角形のひとつの内角は、 1440÷10=144 (度) になります。 あ、前の回答者さんの方が正当ですね。 こちらは別解ということで♪ 7人 がナイス! しています その他の回答(2件) ナイスの多い順 新しい順 古い順4 星形 n 角形の角の和 星形七角形を,内側の七角形の各辺を延長してできた図形と考える。 内側の七角形のまわりにできた7つの三角形の内角の和の合計は,




50 グレア多角形内角 壁紙おしゃれトイレ



科学网 刘瑞祥 我折叠的正多面体 孙冰的博文



正九边形求内角 腾讯视频




新鮮な正10 角形 最高のぬりえ




多角形の内角の和 算数の公式覚えてますか
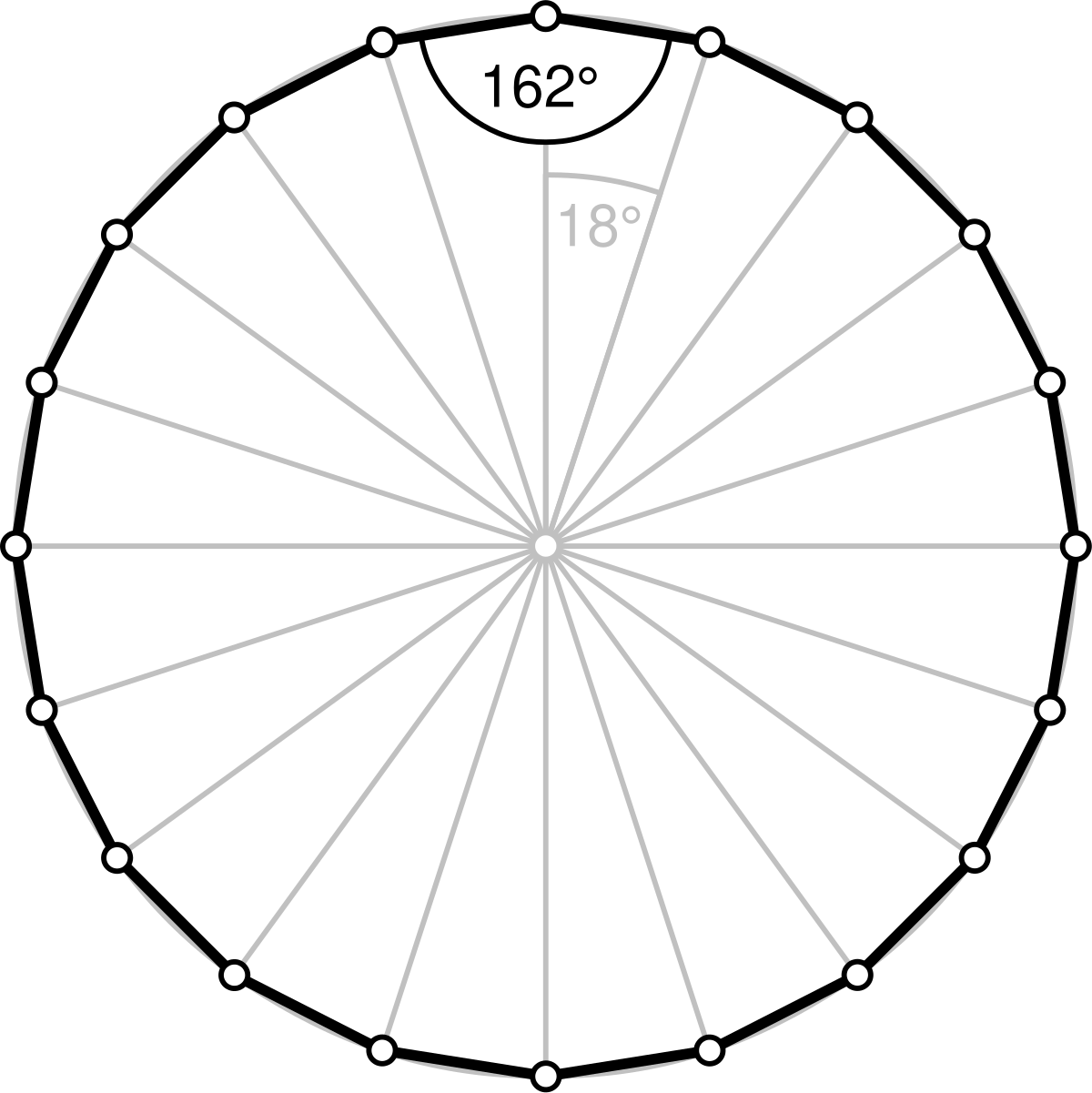



二十边形 维基百科 自由的百科全书



10边形内角和是多少 吾爱中考网




六边形的面积公式有趣的面积问题




联系生活 情景导入 Ppt Download



正九边形求内角 腾讯视频



正十八角形 Japaneseclass Jp




十边形 Wikiwand
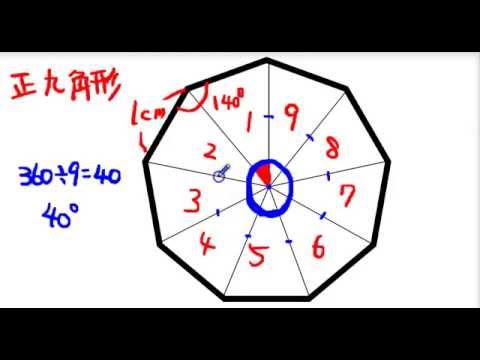



正多角形の性質 正九角形を例に Youtube



新鮮な正10 角形 最高のぬりえ




Python Turtle 画正多边形和多角形 弄斧人y Y的博客 程序员宅基地 Python Turtle画多边形 程序员宅基地



正n角形の内角の和は2 n 2 直角である 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ



五边形的度数是多少




初一下册数学丨多边形的内角和与外角和 每日头条




ベスト50 正12 角形 最高のぬりえ




高中数学知识来推导一下根号2和pi的近似值 步行街主干道 虎扑社区




正十八角形の1つの内角の大きさを求めなさい この問題の解き方教えてください Clear




正多角形




正12 角形 ニスヌーピー壁紙




十六边形内角和 搜狗搜索



正五边形的外角 西瓜视频搜索



正n角形の内角の和は2 n 2 直角である 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ




十角形 Wikipedia




十边形 维基百科 自由的百科全书



Python Turtle 画正多边形和多角形 弄斧人y Y的博客 程序员宅基地 Python Turtle画多边形 程序员宅基地




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




十二边形 全世界条目



正十角形の1つの外角の大きさはどう求めるか教えてください 多 Yahoo 知恵袋




1 Descubre Como Resolverlo En Qanda




维基百科 正十七边形 维基百科 自由的百科全书



Www Study X Com Syotesttyu2 Zukei Takakukeinokaku Pdf



新鮮な正10 角形 最高のぬりえ




無料 中2数学 基本解説 解答プリント 223 図形3 多角形の角




正十二角形の一つの内角はどうやって求めればいいのか教えてください Clear




正十八角形 Japaneseclass Jp




正十二面体体积推导 补 知乎




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく



一个正n边形的每个内角为144 求这个正n边形的所有对角线条数 网易视频



八年级数学竞赛例题专题 多边形的边与角 莲山课件




正多边形 维基百科 自由的百科全书




十一边形 Wikiwand




多角形の内角の和 算数の公式覚えてますか




十一边形 Wikiwand



この問題を教えて下さい 正10角形の1つの内角の大きさを求めるには10角形 Yahoo 知恵袋




小学校5年 算数 正多角形の角の大きさ Youtube




十边形 维基百科 自由的百科全书




八年级数学上册11 3 多边形的内角和与外角和 同步测试 含解析 新版 新人教版下载 Word模板 爱问共享资料



十四边形 Wikiwand




Mathematics 解き方見ても自分の答えと全然一致しません Clear




九年级数学正多边形和圆人教四年制下载 Word模板 爱问共享资料
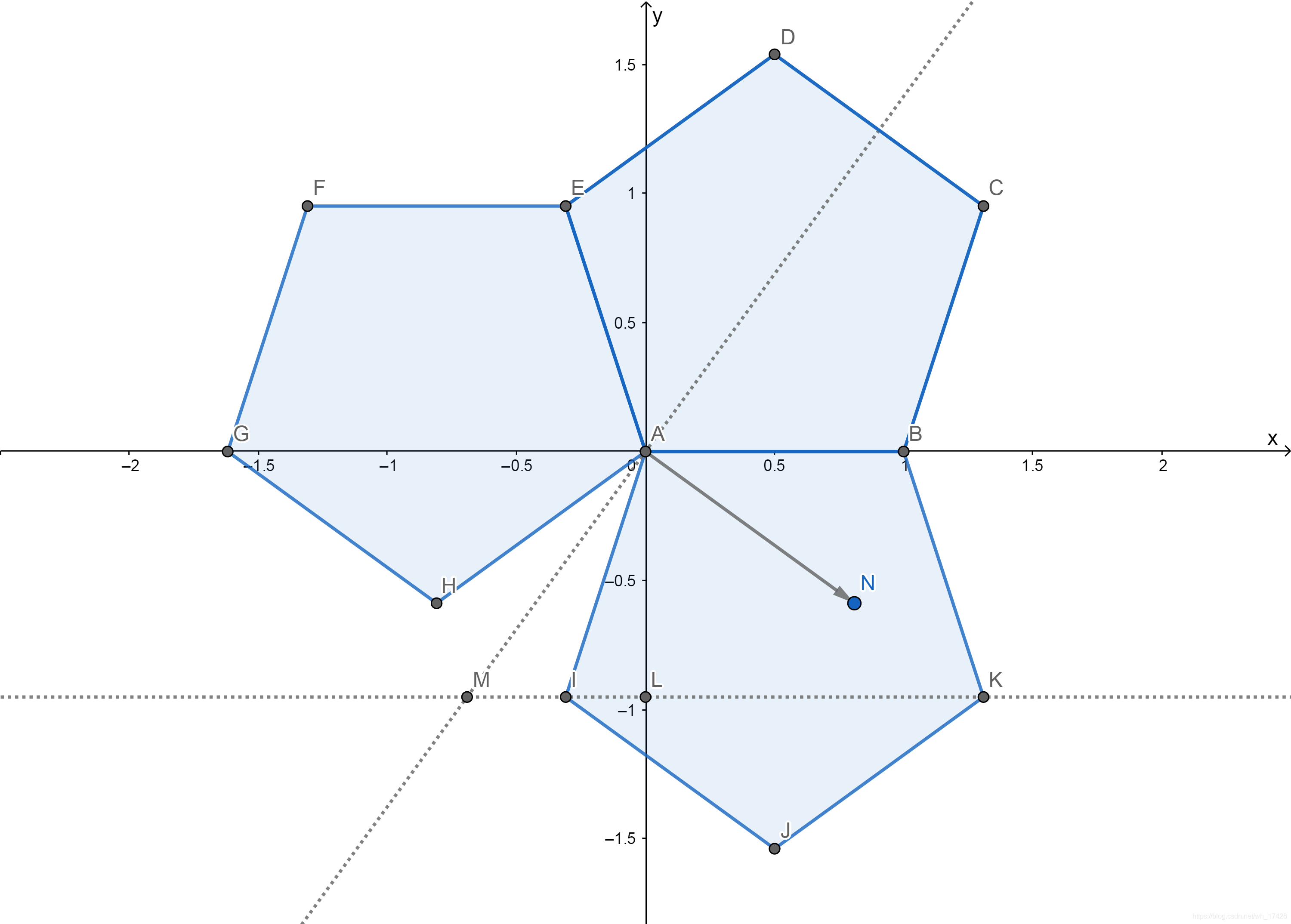



正十二面体二面角的一种求法 Wh 的博客 Csdn博客
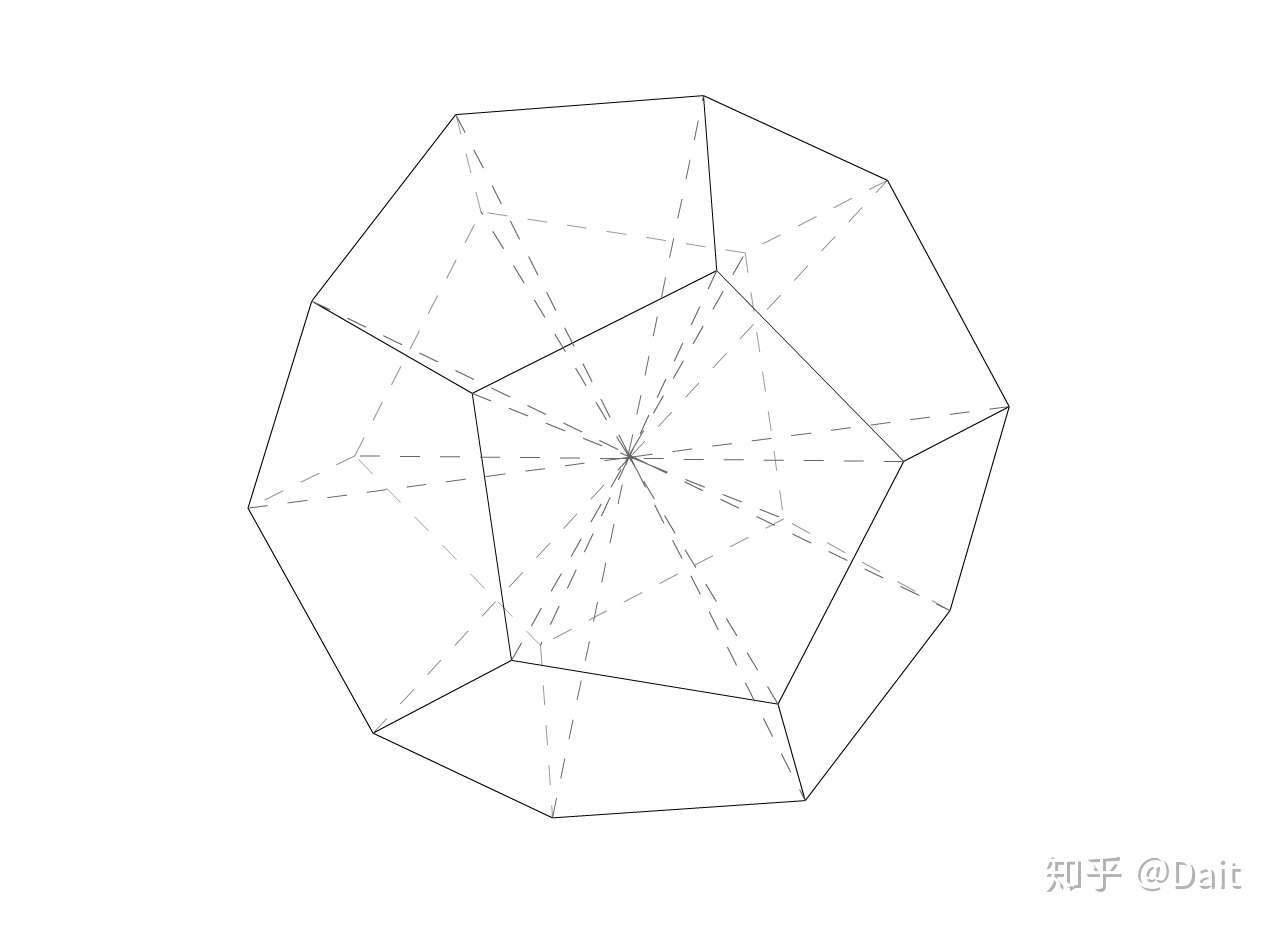



正十二面体体积推导 补 知乎




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく



10边形第1页 驾考预约大全




十边形的画法步骤图 正十边形要怎么画 三人行教育网 Www 3rxing Org
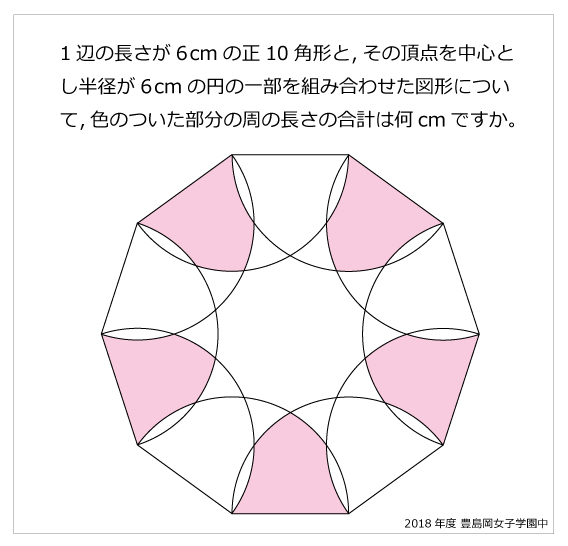



新鮮な正10 角形 最高のぬりえ



正十二边形内角和 搜狗搜索




1 Descubre Como Resolverlo En Qanda




十角形の対角線 アセント学習塾 塾長の こうかい 日誌



N边形的内角和 西瓜视频搜索




Python Turtle 画正多边形和多角形 弄斧人y Y的博客 程序员宅基地 Python Turtle画多边形 程序员宅基地




正多角形の1つの内角 外角を求める方法を問題解説 数スタ




Python Turtle 画正多边形和多角形 弄斧人y Y的博客 程序员宅基地 Python Turtle画多边形 程序员宅基地



Http Www Asahikawa Hkd Ed Jp Nagayama Jhs 221 Ef 92 E5 B9 B4 E6 95 B0 E5 Ad A6 Ef E5 9b E5 80 80 E5 9a E8 92 E5 81 Ae E5 86 85 E8 92 81 A8 E5 96 E8 92 80 80 E8 A3 E7 Ad 94 Ef Pdf



正12 角形 ニスヌーピー壁紙




08年学业考试复习第一轮第四章基本图形一知识回顾多边形上或内部一点与多边形各顶点的连线将多边形分割成若干个小三角形如图给出了四边形的三种不同的分割方法分别将四边形分割成了2个3个4个小三角形
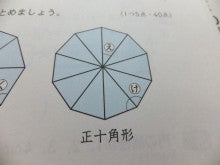



多角形の内角の和で なるほど 今日も 明日も ママヂカラ



求风筝图形内角度数 为什麽角2 角4如图案所示 2 4 5个风筝形拼成一个正10边形 所以 1 10 2 180 10 8 180 144 5 3 360 3 72 风筝形是个四边形 内角和是360度 并且 2 4 所以 作业 慧海网




多边形的内角




360边形
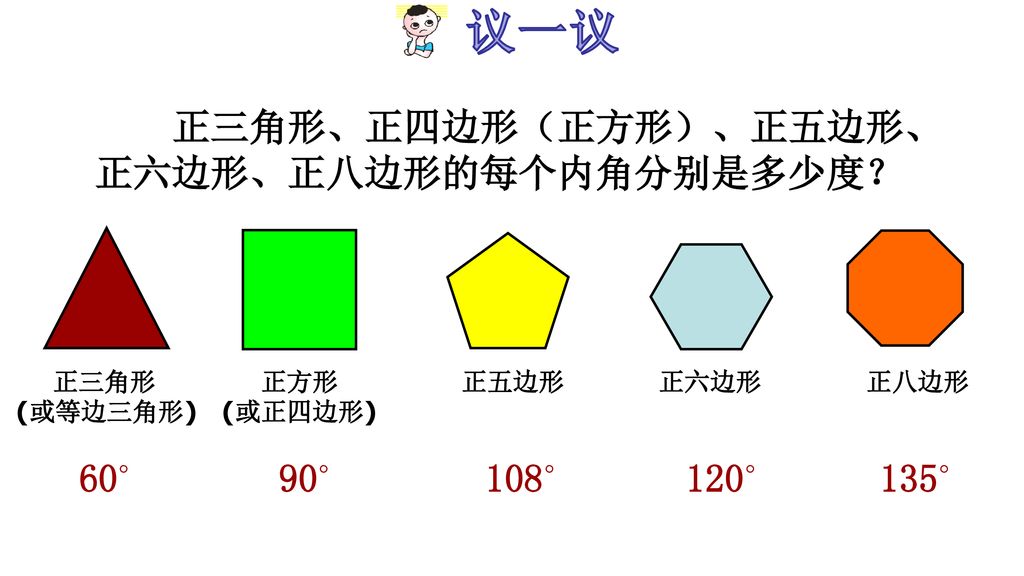



联系生活 情景导入 Ppt Download



正十二边形内角度数 搜狗搜索




八角形正多边形内角六边形不规则线png图片素材免费下载 图片编号 Png素材网



12边形 万图壁纸网



Python绘图实例5 正十二边形绘制 简时刻的博客 Csdn博客




十角星 Wikiwand



九边形内角和是多少度 信息阅读欣赏 信息村 K0w0m Com



十边形 万图壁纸网
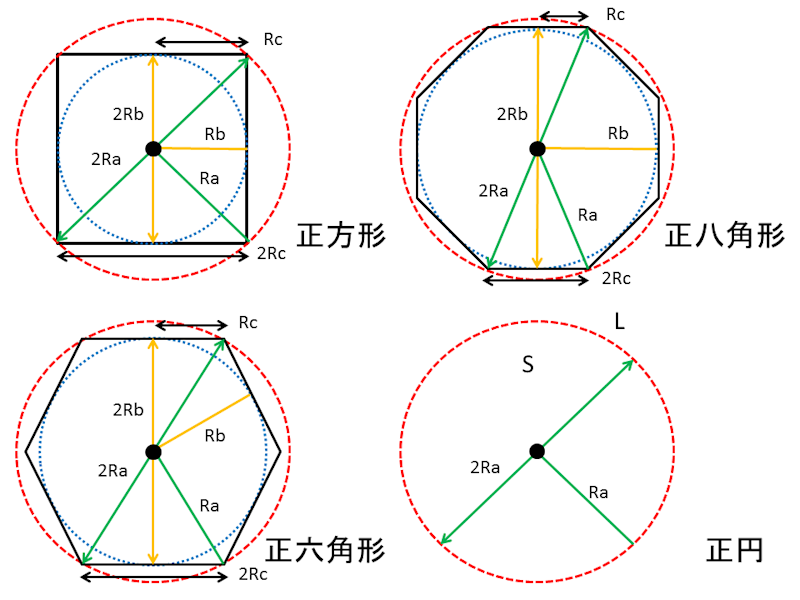



正多角形 Color Cube ウィキ Atwiki アットウィキ




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



Python Turtle 画正多边形和多角形 弄斧人y Y的博客 程序员宅基地 Python Turtle画多边形 程序员宅基地


